Reading Ma 2004 Chapter 2.2-2.3

Motion examples

1. Translation \[\vec{x}' = \vec{x}+\vec{t}\]
2. Rotation \[\vec{x}' = \vec{x}\cdot R\]
   • But note that \(R\) is not an arbitrary matrix.
   • We’ll return to the restrictions

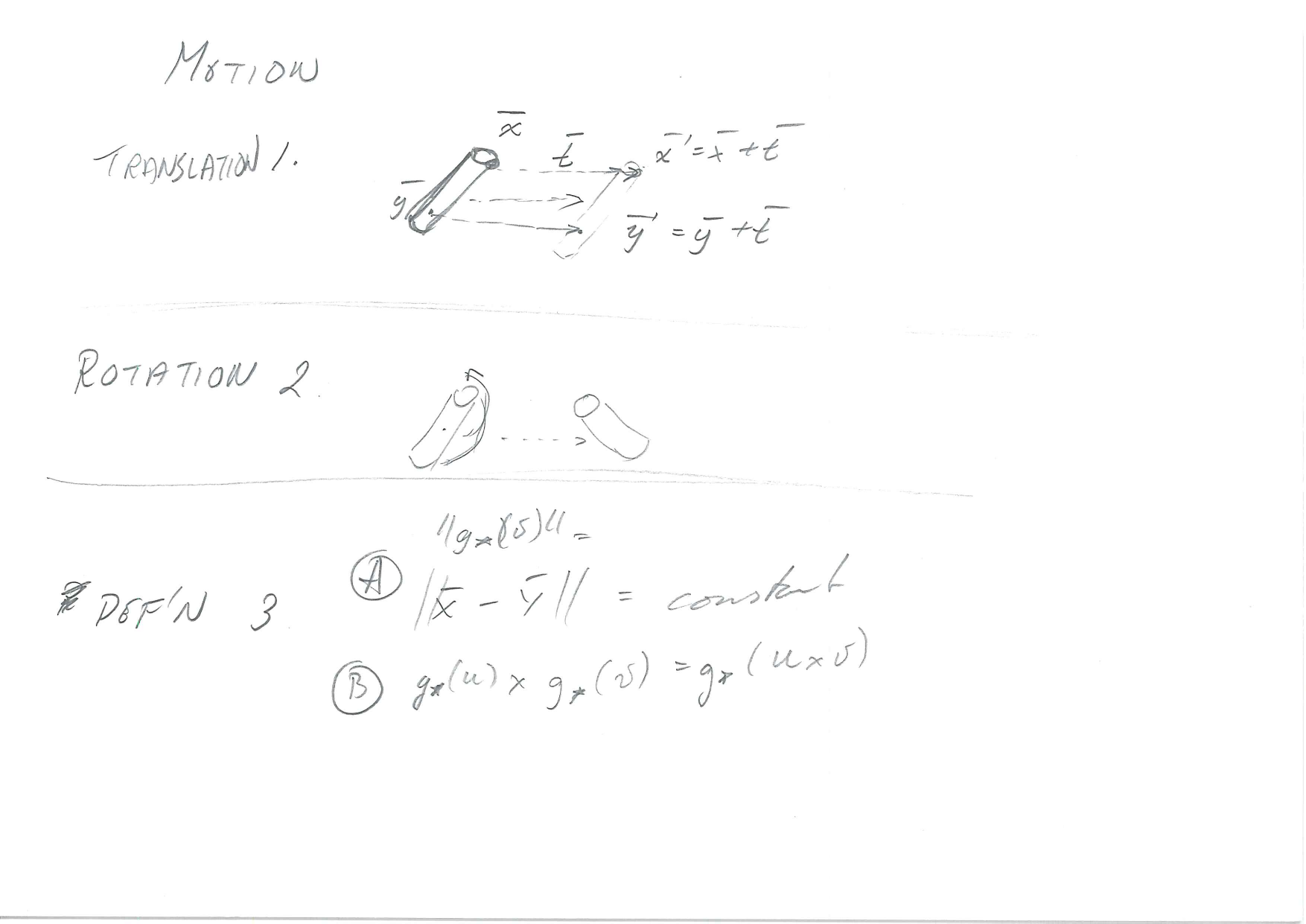
Definition: Rigid Body Motion

1. 3D Object is a set of points in \(\mathbb{R}^3\)
2. If the object moves, the constituent points move
3. The points have to move so that they preserve the shape of the object

Constraints

Let \(\vec{X}(t)\) and \(\vec{Y}(t)\) be the coordinates of points \(\vec{x}\) and \(\vec{x}\) at time \(t\).

1. Preserve distance between points
   • \(||\vec{X}(t)-\vec{Y}(t)||\) is constant
2. Preserve orientation
   • i.e. avoid mirroring
   • we have to preserve cross-products
   • If the right hand rule turns into a left hand rule, we have had mirroring.

Let \(u=\vec{X}-\vec{Y}\) be a vector, and \(g_*(u)=g(\vec{X})-g(\vec{Y})\) the corresponding vector after motion.

Preserving the cross-product means \[g_*(u)\times g_*(v) = g_*(u\times v), \forall u,v\in\mathbb{R}^3\]

Change of Basis

Bases

1. Basis aka. frame
   • Unit vectors: \(\vec{e}_1\), \(\vec{e}_2\), \(\vec{e}_3\)
2. The meaning of a tuple to denote a vector
   • \(\vec{x}=[x_1,x_2,x_3]= x_1\cdot\vec{e}_1+x_2\cdot\vec{e}_2+x_3\cdot\vec{e}_3\)
3. Orthonormal frame: orthogonal and unit length \[\vec{e}_i\vec{e}_j=\delta_{ij} = \begin{cases} 1 \quad\text{if } i=j\\ 0 \quad\text{if } i\neq j \end{cases} \]

Local and Global Basis

1. 3D Scenes are built hierarchically
2. Each object is described in a local basis
   • and then placed in the global basis.
3. Why?
   • Save computational work
   • Local changes affect only local co-ordinates
   • Component motion independent of system motion

Example

E.g. our co-ordinates: 62°28’19.3“N 6°14’02.6”E

Are these local or global co-ordinates?

Rotation

Consider common origin first.