Revision e0c8d4321c3d5fd522bfa51d231bf06622752661 (click the page title to view the current version)
Change of Basis
Reading Ma 2004 Chapter 2.2-2.3
Motivation
- Complex scene.
- Lots and lots of points.
- If an object moves, all its points changes.
- This is unmanageable
- Modularise
- Describe the object in local co-ordinates.
- Describe the location and orientation of the object once in the global co-ordinate system.
- When the object moves, its local co-ordinate system changes relative to the global one, but the internal description of the object does not.
Motion examples
Demo
- Translation \[\vec{x}' = \vec{x}+\vec{t}\]
- Rotation \[\vec{x}' = \vec{x}\cdot R\]
- But note that \(R\) is not an arbitrary matrix.
- We’ll return to the restrictions
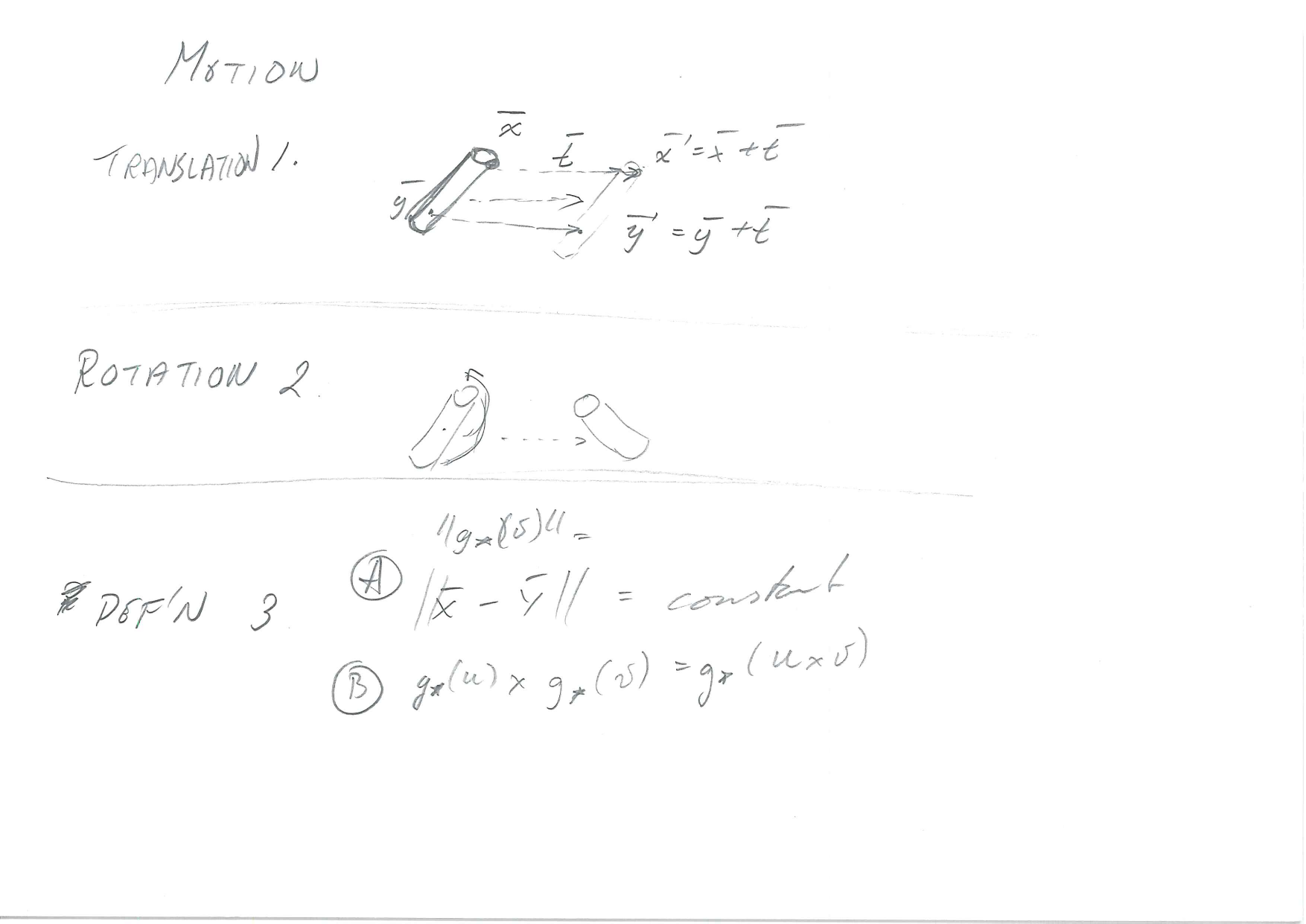
Definition: Rigid Body Motion
- 3D Object is a set of points in \(\mathbb{R}^3\)
- If the object moves, the constituent points move
- The points have to move so that they preserve the shape of the object
Constraints
Let \(\vec{X}(t)\) and \(\vec{Y}(t)\) be the coordinates of points \(\vec{x}\) and \(\vec{x}\) at time \(t\).
- Preserve distance between points
- \(||\vec{X}(t)-\vec{Y}(t)||\) is constant
- Preserve orientation
- i.e. avoid mirroring
- we have to preserve cross-products
- If the right hand rule turns into a left hand rule, we have had mirroring.
Let \(u=\vec{X}-\vec{Y}\) be a vector, and \(g_*(u)=g(\vec{X})-g(\vec{Y})\) the corresponding vector after motion.
Preserving the cross-product means \[g_*(u)\times g_*(v) = g_*(u\times v), \forall u,v\in\mathbb{R}^3\]
Change of Basis
Bases
- Basis aka. frame
- Unit vectors: \(\vec{e}_1\), \(\vec{e}_2\), \(\vec{e}_3\)
- The meaning of a tuple to denote a vector
- \(\vec{x}=[x_1,x_2,x_3]= x_1\cdot\vec{e}_1+x_2\cdot\vec{e}_2+x_3\cdot\vec{e}_3\)
- Orthonormal frame: orthogonal and unit length \[\vec{e}_i\vec{e}_j=\delta_{ij} = \begin{cases} 1 \quad\text{if } i=j\\ 0 \quad\text{if } i\neq j \end{cases} \]
Arbitrary Choice of Basis
- Any set of three linearly independent vectors \(\vec{u}_1\), \(\vec{u}_2\), \(\vec{u}_3\) can be used as a basis.
- Usually, we prefer an orthonormal basis, i.e.
- the basis vectors are orthogonal
- the basis vectors have unit length
\[ \langle\vec{u}_i, \vec{u}_j\rangle = \begin{cases} 1, \quad\text{when } i=j,\\ 0, \quad\text{when } i\neq j\end{cases}\]
- The basis is relative to a given Origin
Local and Global Basis
- 3D Scenes are built hierarchically
- Each object is described in a local basis
- and then placed in the global basis.
- Why?
- Save computational work
- Local changes affect only local co-ordinates
- Component motion independent of system motion
Describing a Scene
- Each object described in its own basis
- independently of its position and orientation in the scene
- reusable objects
- Rotation and Deformation can be described locally
- Transformation from local to global co-ordinates
- Rotation of the basis
- Translation of the origin
- System of Systems
- an object in the scene may itself be composed of multiple objects with different local frames
Example
E.g. our co-ordinates: 62°28’19.3“N 6°14’02.6”E
Are these local or global co-ordinates?
Rotation
Consider common origin first.
Working with Different Bases
Change of Basis
- Point \(\vec x\) represented in a basis \(\vec{e}_1\), \(\vec{e}_2\), \(\vec{e}_3\)
- i.e. \(\vec x = x_1\vec{e}_1 + x_2\vec{e}_2 + x_3\vec{e}_3\)
- Translate to a representation in another basis \(\vec{u}_1\), \(\vec{u}_2\), \(\vec{u}_3\)
- Suppose we can write the old basis in terms of the new one
- \(\vec{e_i} = e_{i,1}\vec{u}_1 + e_{i,2}\vec{u}_2 + e_{i,3}\vec{u}_3\)
\[\begin{split} p = & x_1(e_{1,1}\vec{u}_1 + e_{1,2}\vec{u}_2 + e_{1,3}\vec{u}_3) + \\ & x_2(e_{2,1}\vec{u}_1 + e_{2,2}\vec{u}_2 + e_{2,3}\vec{u}_3) + \\ & x_3(e_{3,1}\vec{u}_1 + e_{3,2}\vec{u}_2 + e_{3,3}\vec{u}_3) \\ = &(x_1e_{1,1} + x_2e_{2,1} + x_3e_{2,1} )\vec{u}_1 + \\ &(x_1e_{1,2} + x_2e_{2,2} + x_3e_{2,2} )\vec{u}_2 + \\ &(x_1e_{1,3} + x_2e_{2,3} + x_3e_{2,3} )\vec{u}_3 \end{split}\]
Write \([x'_1, x'_2, x'_3]^\mathrm{T}\) for the coordinates in terms of the new basis.
\[ x'_i = x_1e_{1,i} + x_2e_{2,i} + x_3e_{2,i} \]
- In matrix form we can write \[p = [x_1',x_2',x_3'] = [ \vec{e}_1 | \vec{e}_2 | \vec{e}_3 ]\cdot\vec{x}\] where \(\vec{e}_i\) are written as column vectors.
Orthonormal matrix
\[R = [ \vec{e}_1 | \vec{e}_2 | \vec{e}_3 ]\]
- Orthonormal basis means that \(R\cdot R^T = R^T\cdot R=I\)
- Hence \(R^{-1}=R^T\)
- If \(\vec{x}'=\vec{x}\cdot R\) then \(\vec{x}=\vec{x}'\cdot R^T\) then
- If the columns of \(R\) make up the new basis,
- then the rows make up the old basis
Example
\[ \begin{split} R = \begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} & 0 \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{split} \]
Note this is orthogonal. Compare it to
Example in 2D
The principle is the same in 2D.
\[ R_1 = \begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ \end{bmatrix} \quad R_2 = \begin{bmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \end{bmatrix} \]
Note that
- \(\frac{\sqrt2}{2}=\sin(\pi/4)=\cos(\pi/4)\).
- \(R_1^TR_1=I\) and \(R_2R_2=I\)
- The determinants \(|R_1|=1\) and \(|R_2|=-1\)
Consider a triangle formed by the points \((0,0)\), \((0,1)\), \((1,1)\), and consider each of them rotated by \(R_1\) and \(R_2\)
Rotation around an axis
A rotation by an angle \(\theta\) around the origin is given by \[ R_\theta = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \\ \end{bmatrix} \] In 3D, we can rotate around a given axis, by adding a column and row to the 2D matrix above. E.g. to rotate around the \(y\)-axis, we use \[ R_\theta = \begin{bmatrix} \cos\theta & 0 & -\sin\theta \\ 0 & 1 & 0 \\ \sin\theta & 0 & \cos\theta \\ \end{bmatrix} \]
Operations on rotations
- If \(R_1\) and \(R_2\) are rotational matrices, then \(R=R_1\cdot R_2\) is a rotational matrix
- There is an identity rotation \(I\)
- If \(R_1\) is a rotational matrices, then there is an inverse rotation \(R_1^{-1}\)
- If \(R_1\), \(R_2\), and \(R_3\) are rotational matrices, then \(R_1(R_2R_3)= (R_1R_2)R_3\)
Rotation as Motion
Why is change of basis so important?
- It also describes rotation of rigid bodies
- To rotate a body, rotate its local basis
- Any orthonormal basis is a rotation of any other
- The matrix \(R\) defines the rotation
- Any orthogonal matrix defines a rotation
Demo
Use Python Here
Moving the Origin
- A point is described relative to the origin
\[\mathbf x = \mathbf{0} + x_1\cdot\vec{e}_1 + x_2\cdot\vec{e}_2 + x_3\cdot\vec{e}_3\]
- Note that I write \(\mathbf{x}\) for a point and \(\vec{x}\) for a vector
- The origin is arbitrary
- The local co-ordinate system is defined by
- the basis \(\vec{e}_1\), \(\vec{e}_2\), \(\vec{e}_3\)
- the origin \(\mathbf{0}\)
- Move origin: \(\mathbf{0}'=\mathbf{0}+\vec{t}\)
- for some translation vector \(\vec{t}\)
Arbitrary motion
- \(\mathbf{X}\mapsto \mathbf{X}\cdot R + \vec{t}\)
- or \(\mathbf{X}\mapsto (\mathbf{X}-\vec{t}_1)\cdot R + \vec{t}_2\)
- remember, what is the centre of rotation?
