Machine Vision

Introductory Session

Hans Georg Schaathun

NTNU, Noregs Teknisk-Naturvitskaplege Universitet

21 August 2023

  1. Briefing Overview and History
  2. Install and Test Software - Simple tutorials
  3. Debrief questions and answers recap of linear algebra

Introduction

  • What is your name?
  • Why do you take this module?

Practical Information

Questions - either in class or in discussion fora

Taught Format

  • Sessions 4h twice a week
    • 1h briefing + 2h exercise + 1h debrief (may vary)
  • Variety of exercise genres
  • No Compulsory Exercises
    • but not less work
  • Feedback in class
    • please ask for feedback on partial work
  • Keep a diary.
    • Highlight your take-aways
    • Remember partial solution for reuse
  • Use the textbooks to learn what you need to do
    • Not as a checklist of what you need to learn

Learning Outcomes

Knowledge
  • The candidate can explain fundamental mathematical models for digital imaging, 3D models, and machine vision
  • The candidate are aware of the principles of digital cameras and image capture
    • Skills
  • The candidate can implemented selected techniques for object recognition and tracking
    • General competence
  • The candidate has a good analytic understanding of machine vision and of the collaboration between machine vision and other systems in robotics
  • The candidate can exploit the connection between theory and application for presenting and discussing engineering problems and solutions

    • Exam

    • Oral exam \(\sim 20\) min.
    • First seven minutes are yours
      • make a case for your grade wrt. learning outcomes
      • your own implementations may be part of the case
      • essentially that you can explain the implementation analytically
    • The remaing 13-14 minutes is for the examiner to explore further
    • More detailed assessment criteria will be published later

    Vision

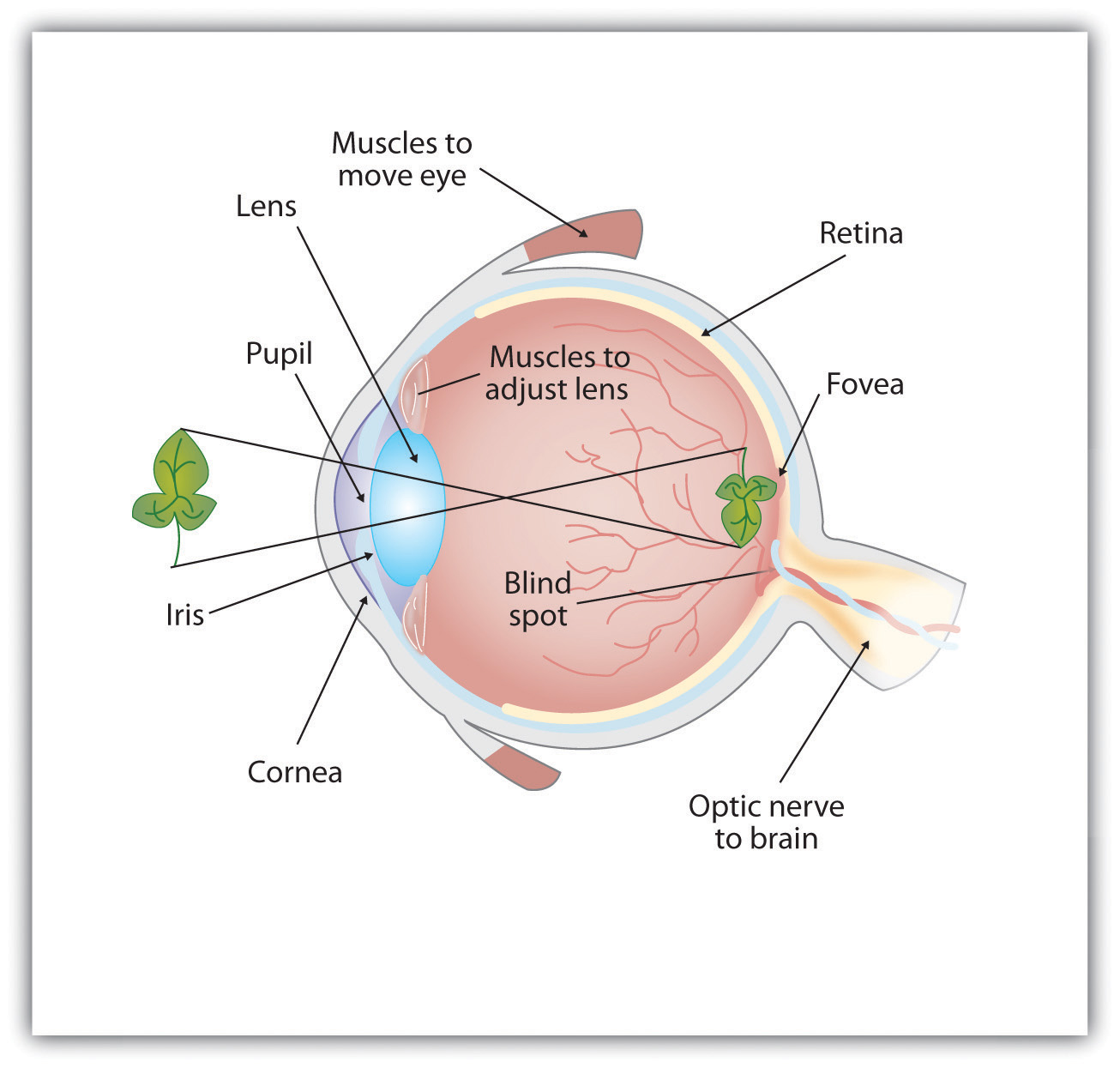
    Eye Model from Introduction to Psychology by University of Minnesota

    • Vision is a 2D image on the retina
      • Each cell perceives the light intencity of colour of the light projected thereon
    • Easily replicated by a digital camera
      • Each pixel is light intencity sampled at a given point on the image plane

    Cognition

    1912 International Lawn Tennis Challenge

    • Human beings see 3D objects
      • not pixels of light intencity
    • We recognise objects - cognitive schemata
      • we see a ball - not a round patch of white
      • we remember a tennis match - rather than four people with white clothes and rackets
    • We observe objects arranged in depth
      • in front of and behind the net
      • even though they are all patterns in the same image plane
    • 3D reconstruction from 2D retina image
      • and we do not even think about how

    Applications

    • Artificial systems interact with their surroundings
      • navigate in a 3D environment
    • Simpler applications
      • face recognition
      • tracking in surveillance cameras
      • medical image diagnostics (classification)
      • image retrieval (topics in a database)
      • detecting faulty products on a conveyor belt (classification)
      • aligning products on a conveyor belt
    • Other advances in AI creates new demands on vision
      • 20 years ago, walking was a major challenge for robots
      • now robots walk, and they need to see where they go ...

    By Adrian Rosebrock , CC BY-SA 4.0,wikimedia commons

    Wikimedia

    200~By NASA on The Commons No restrictions,Wikimedia Commons

    Focus for the module

    • Artificial systems interact with their surroundings
      • navigate in a 3D environment
    • This means
      • Geometry of multiple views
      • Relationship between theory and practice
      • ... between analysis and implementation
    • Mathematical approach
      • inverse problem; 3D to 2D is easy, the inverse is hard
      • we need to understand the geometry to know what we program

    Subproblems

    • 3D modelling
      • Linear Algebra
    • Distortion and calibration
      • 2D Geometry
    • Feature detection
      • image (signal) processing
      • possibly machine learning

    Big Problem

    Vision System

    i.e. putting it all together

    History

    • 1435 Della Pictura - first general treatise on perspective
    • 1648 Girard Desargues - projective geometry
    • 1913 Kruppa: two views of five points suffice to find
      • relative transformation
      • 3D location of the points
      • (up to a finite number of solutions)
    • mid 1970s first algorithms for 3D reconstruction
    • 1981 Longuet-Higgins: linear algorithm for structure and motion
    • late 1970s E. D. Dickmans starts work on vision-based autonomous cars
    • 1984 small truck at 90 km/h on empty roads
    • 1994 180 km/h, passing slower cars

    Python

    • Demos and tutorials in Python
      • not Jupyter - we need to interface cameras and interactive displays easily
      • you can use whatever language you want
    • Demos and help on Unix-like system
    • exercise session today
      • install necessary software
      • use the tutorials to see that things work as expected
    • In the debrief, we will start briefly on the mathematical modelling
    1. Quick demo
    2. Do your tutorials - discuss - ask questions
    3. After the exercise we resume for a debrief

    Debrief

    1. What have you learnt from the exercise?
    2. Did you encounter any problems or questions to be discussed?
    3. 3D Mathematics

    Vectors and Points

    A point in space $\mathbf{X} = [X_1,X_2,X_3]^\mathrm{T}\in\mathbb{R}^3$
    A bound vector, from $\mathbf{X}$ to $\mathbf{Y}$$\vec{\mathbf{XY}}$
    A free vector is the same difference, but without any specific anchor pointrepresented as $\mathbf{Y} - \mathbf{X}$
    • Set of free vectors form a linear vector space
      • note! points do not
      • The sum of two vectors is another vector
      • The sum of two points is not a point

    Dot product (inner product)

    $$x=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}\quad y=\begin{bmatrix}y_1\\y_2\\y_3\end{bmatrix}$$

    $$\langle x,y\rangle = x^\mathrm{T}y = x_1y_1+x_2y_2+x_3y_3$$

    Euclidean Norm: $||x|| = \sqrt{\langle x,x\rangle}$

    Orthogonal vectors when $\langle x,y\rangle=0$

    Cross product

    $$x\times y = \begin{bmatrix} x_2y_3 - x_3y_2 \\ x_3y_1 - x_1y_3 \\ x_1y_2 - x_2y_1 \end{bmatrix} \in \mathbb{R}^3$$

    Observe that

    1. $y\times x = -x\times y$
    2. $\langle x\times y, y\rangle= \langle x\times y, x\rangle$

    $$x\times y = \hat xy \quad\text{where}\quad \hat x = \begin{bmatrix} 0 & -x_3 & x_2 \\ x_3 & 0 & -x_1 \\ -x_2 & x_1 & 0 \end{bmatrix} \in \mathbb{R}^{3\times3}$$

    $\hat x$ is a skew-symmetric matrix because $\hat x=-\hat x^\mathrm{T}$

    i.e. the cross-product is a linear operation

    Right Hand Rule

    By Acdx - Self-made, based on Image:Right_hand_cross_product.png,BY-SA 3.0, Wikimedia Commons

    Matrix Arithmetics

    Matrices define linear operations on vectors

    $$ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \\ \end{bmatrix} \cdot \begin{bmatrix} 2 \\ 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 1 \\ 0 \end{bmatrix} $$

    $$ \begin{bmatrix} a_{11} & a_{21} & a_{23} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} a_{11}x_1 & a_{21}x_2 & a_{23}x_3 \\ a_{21}x_1 & a_{22}x_2 & a_{23}x_3 \\ a_{31}x_1 & a_{32}x_2 & a_{33}x_3 \\ \end{bmatrix} $$

    • Change of Basis
    • Rigid Body Motion