• Goal Understand and be able to implement Q-learning
  • Builds on the Markov Decision Process Model MDP from last week.
  • Next week: Deep Q-Learning
• Reading Russel and Norvig Chapter 23
• Eirik’s slides from 2022
• Eirik’s Jupyter Notebook 2022

Exercises

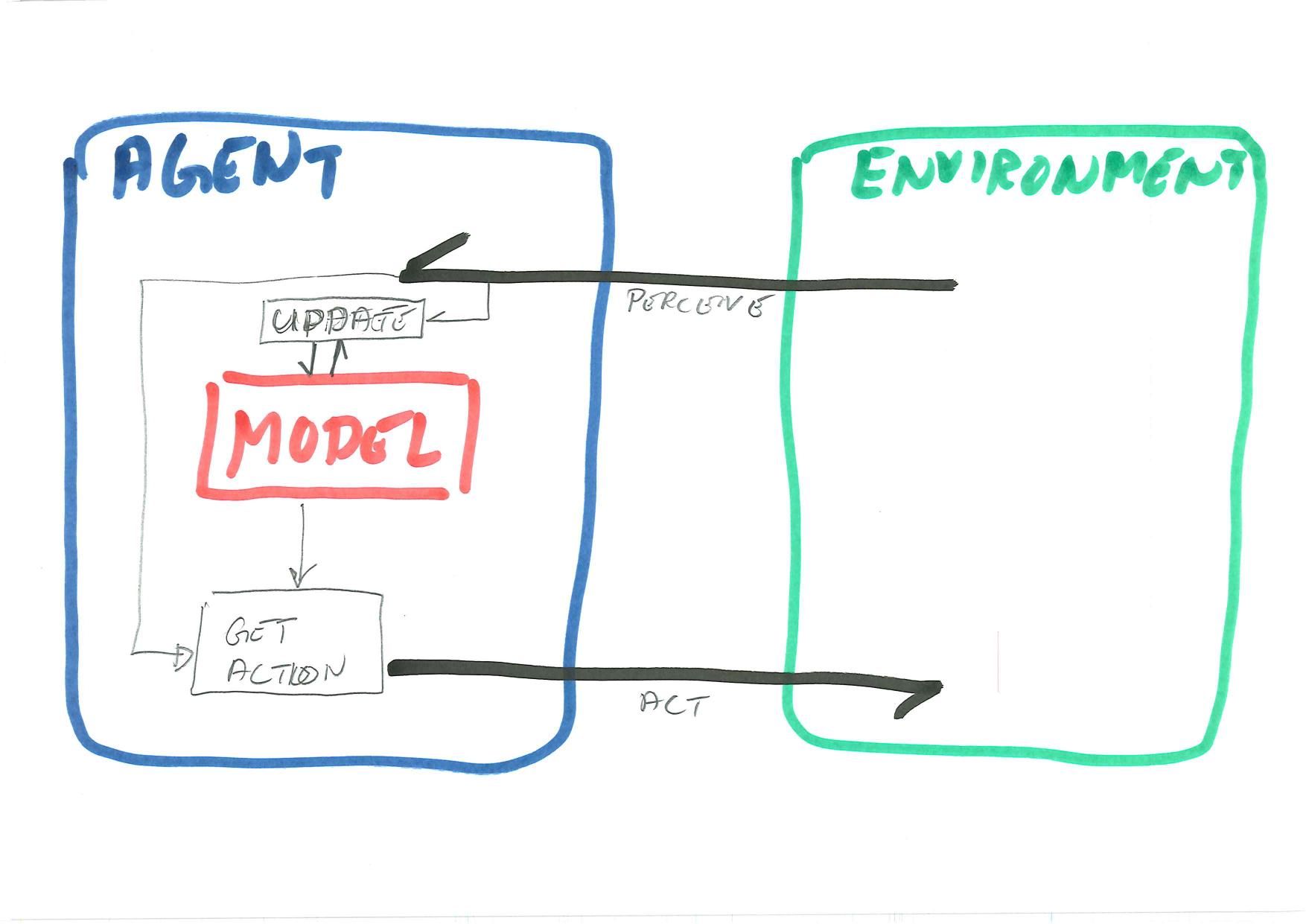
In this session we will create a Reinforcement Learning Agent, as depicted in the diagram. Note the internal model, with one function to update it and one function using it to choose an action. You should keep this picture in your mind throughout.

Last session we discussed the Q-Function, \[Q(s,a) = \sum_{s'}P(s'|s,a)[R(s,a,s') + \gamma \max_{a'}Q(s',a')]\] and the function for the optimal policy based on the results from the Q-Function:
\[\pi^*(s) = \mathop{\text{argmax }}\limits_aQ(s,a)\] We also discussed iterative estimation of the utilities and the policies. This session, we will implement an iterative estimation algorithm for the Q-values, knowns as Q-learning. This is a model-free, off-policy reinforcement learning algorithm.

The exercise outline below is based partly on Eirik’s assigment in 2022 and partly on the Gymnasium tutorial on Blackjack.

Note that I have not asked you explicitly to output any diagnostics on the way. You almost certainly have to do this yourself, so that you know what is going on.

Goal and overvew

The goal for this session is to implement an agent that can solve the Frozen Lake problem as well as possible, using Q-learning. The skeleton for the Agent will look like this:

class Agent:
    def __init__( self, env, learning_rate=0.1,
        initial_epsilon=1.0, epsilon_decay=10**(-50000),
        final_epsilon=0.1, discount_factor=0.95):
        pass
    def get_action(self, obs):
        pass
    def update( self, obs, action, reward, terminated, next_obs):
        pass
    def decay_epsilon(self):
        pass

Thus we need four methods. The most obvious ones are the constructor, the move generator, and model updater. The last method reduces \(\epsilon\) which is the probability of making a random move instead of the best move according to the model.

In order to run the model, you can use the following script:

import matplotlib.pyplot as plt
from Agent import Agent

import gymnasium as gym

env = gym.make('FrozenLake-v1', desc=None, map_name="4x4", is_slippery=False,render_mode="human")

done = False
observation, info = env.reset()

action = env.action_space.sample()
observation, reward, terminated, truncated, info = env.step(action)

agent = Agent( env )

for episode in range(30):
    obs, info = env.reset()
    done = False

    # play one episode
    while not done:
        action = agent.get_action(obs)
        next_obs, reward, terminated, truncated, info = env.step(action)

        # update the agent
        agent.update(obs, action, reward, terminated, next_obs)

        # update if the environment is done and the current obs
        done = terminated or truncated
        obs = next_obs

    agent.decay_epsilon()

Note We have set is_slippery=False above. That’s useful for the initial testing; we will change it to True later.

Note 2 We use 30 episodes. This is ridiculously little, but the animation is slow, and we need to be able to run it several times in testing.

Note 3 You can turn off the animation by changhing to render_mode="array". This is a lot faster, but you will need some other way to see what is going on.

1. Constructor

Implement the constructor. You need to record all the parameters and initialise the Q-table. You can use Eirik’s initial Q-values below, or it is also possible to use a defaultdict as does the Blackjack tutorial.

initalQ = np.array([  
		[0.009, 0.192, 0.007, 0.009],  
		[0.003, 0.002, 0.003, 0.17],  
		[0.003, 0.002, 0.001, 0.067],  
		[0.001, 0.001, 0.002, 0.037],  
		[0.526, 0.002, 0.001, 0.002],  
		[0., 0., 0., 0.],  
		[0.046, 0., 0., 0.],  
		[0., 0., 0., 0.],  
		[0.002, 0.002, 0.002, 0.709],  
		[0.001, 0.597, 0.001, 0.001],  
		[0.945, 0., 0., 0.],  
		[0., 0., 0., 0.],  
		[0., 0., 0., 0.],  
		[0.02, 0.012, 0.898, 0.016],  
		[0.061, 0.991, 0.092, 0.068],  
		[0., 0., 0., 0.]  
	])  

In this format initialQ[state][action] is the tenative value for \(Q\)(state,action).

2. Move generator

The move generator get_action() has to return a valid action, that is an integer in the 0–3 range for the Frozen Lake problem. With probability \(\epsilon\) you want to return a random action (see last session for code example), and with probability \(1-\epsilon\), the action which maximises \(Q\) according to the current estimate.

• Implement get_action().
• Test the simulator. It should work already at this stage.
• Test it also starting_epsilon=0, so that you can see what happens when it avoids the random moves altogether.

This move generator is known as the Epsilon-Greedy Algorithm. It makes a greedy choice except with \(\epsilon\) probability.

3. Diagnostic output

• Add code to count the number of times you win the game.
• Turn off the animation and increase the number of episodes.
• Is the default strategy able to win the game ever?

4. Model updater

Now we need some way to update the Q-table.
Q-learning is based on one very simple update rule: \[Q(s,a) \leftarrow Q(s,a) + \alpha\left(\left[ R(s,a,s') + \gamma \max\limits_{a'}Q(s',a')\right] - Q(s,a)\right),\] where \(\alpha\) is the learning rate, which controls the speed of convergence.

• Look at the correction term in the update rule (the parenthesis multiplied by \(\alpha\)). Are all the quantities known to the agent? What are the corresponding variables in python?
• Implement update()

5. Epsilon decay

self.epsilon = max(self.final_epsilon, self.epsilon - self.epsilon_decay)

• What does the above line do?
  
• Do the attribute name match the ones you have used?
• Implement decay_epsilon().
• Reflect: Why should \(\epsilon\) decline during training?

6. Testing

• Test the system. Add more diagnostic output as required..
  • Turn the animation off to be able to test realistically.
• Try both Eirik’s default Q-table and one initialised with zeroes only. Does this matter a lot?
• Does the Q-table change a lot during training?
• What happens when you change the training parameters (input to the Agent constructor)?

7. The slippery ice

Change the environment to be slippery

environment = gym.make('FrozenLake-v1', desc=None, map_name="4x4", is_slippery=False)  

• Repeat the tests from 1F. What do you observe?

8. The slippery ice

• Reflect upon your solution.
• What are the key elements of Q-learning?
• Which design decisions are critically to make Q-learning work?
• Is Q-learning an appropriate solution to the problem?

9. Optional

Adapt your solution for other problems in Gymnasium, such as Blackjack.