3D Mathematics
- [Previous: Introduction]-[Up: Overview]-[Next: 3D Objects in Python]
Reading
- Ma (2004) Chapter 2 until Section 2.3 inclusive
- Ma (2004) Appendix A if necessary to understand Chapter 2.
- (Szeliski 2022 Chapter 2 until Section 2.1.3 inclusive)
- Szeliski is a lot briefer, for better or for worse
Briefing
Exercises
Everybody nneds to understand and be able to do the first to problems (turntable and crane). Take time to make sure that you can see the link between the real world geometry and the mathematical methods.
The remaining problems are purely abstract. It is ok if you do not have time to do them, but mastering them will make it easier to take advantage of mathematical models later in the module.
A stage turntable
Let’s try a little 2D exercise before we move to 3D. Consider a theatre stage with a turntable.
The global co-ordinate system is defined with the origin at a seat in the middle of the audience. The \(y\)-axis points directly towards the stage, and the \(x\)-axis is perpendicular, pointing towards the right hand side.
The turntable has its centre at \((0,10)\) in the global co-ordinate system. The centre of the turntable is also the origin of its local co-ordinate system. An actor stands on the turntable at the point \((0,1)\) in the local co-ordinate system.
- Draw and annotate the situation.
- Suppose first that the turntable is turned so that its local \(y\)-axis is aligned with the global one. Where is the actor located in the globale co-ordinate system
- Suppose the turntable turns clockwise by an angle \(\alpha\). Write down the corresponding rotation matrix.
- What becomes the new position of the actor in the global co-ordinate system?
- An actress was positioned at some local co-ordinates \((x,y)\). What is her global position before and after the rotation by \(\alpha\).
- Note that you can calculate the positions of the two actors either directly by simple geometric observations and by means of linear algebra and a change of basis. You should try both and compare the results for validation.
A crane
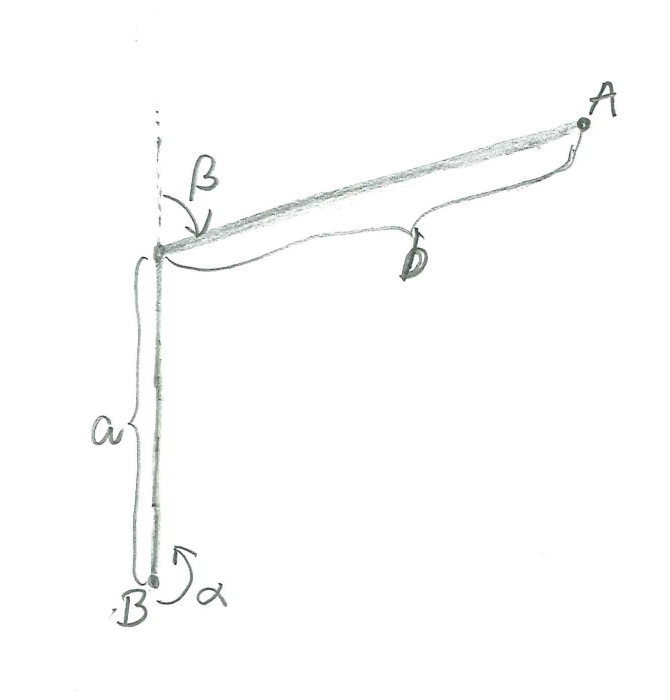
Imagine a crane or robot arm with two booms as shown in the figure. We want to calculate the position of the hand of the arm (i.e. point \(A\)), given the position of the two joints.
- The first boom
- has its base in the global origin.
- can rotate around the \(z\)-axis (the vertical axis).
- has length \(a\) and extends along the \(z\)-axis.
- The second boom
- has its base at the tip of the first boom.
- has length \(b\).
- is jointed so that it can rotate around the \(y\)-axis. Note that this is the \(y\)-axis in the local co-ordinate system of the first boom, which may rotate in the global co-ordinate system.
- Write \(\alpha\) for the angle of rotation around the base. Assume that the boom is in the \(xz\)-plane when \(\alpha=0\).
- Write \(\beta\) for the angle in the joint. Suppose the second boom extends vertically when \(\beta=0\).
Note that each joint and boom can be described in a local co-ordinate system induced by the preceeding joints and booms in the system.
Step 1. Some concrete numbers
Suppose \(a=1\), \(b=2\), and \(\alpha=0\). Let \(\beta=\pi/4\) so that the second boom is horisontal. Draw this situation and calculate the global co-ordinates of the hand (\(A\)).
General solution
Now we will work with general algebraic values, \(a\), \(b\), \(\alpha\), and \(\beta\). To calculate the position of \(A\), we should start with the hand in a local co-ordinate system and work backwards towards the base.
Step 2. The co-ordinate system of the joint
Point \(A\) is the origin in the co-ordinate system of the hand.
- Calculate its position of \(A\) in the co-ordinate system of the joint.
Note that this comprises a translation along the boom, and a rotation by \(\alpha\). You need to specify these two transformations and the order in which to apply them, to arrive at the transformation between the two co-ordinate systems.
Note that each change of co-ordinate system comprises a rotation and a translation. If you prefer, you may consider four distinct co-ordinate systems (instead of two) such that each change of basis makes either a rotation or a translation.
Step 3. The co-ordinate system of the base
- Calculate its position of \(A\) in the co-ordinate system of the base.
To find \(A\) in the global (base) co-ordinate system, we need to find the transformation between the joint basis and the base basis, and combine this with the transformation from base 2.
Properties of the rotation matrix.
This is based on Exercise 2.6 from Ma (2003:38).
Consider two transformation matrices:
\[ R_1= \begin{bmatrix} \cos \theta & -\sin\theta \\ \sin\theta & \cos \theta \end{bmatrix} \quad R_2= \begin{bmatrix} \sin \theta & \cos\theta \\ \cos\theta & -\sin \theta \end{bmatrix} \]
- For each matrix, what is the determinant?
- For each matrix, is it orthogonal?
Consider two points \(\vec{a}=(1,1)\) and \(\vec{b}=(0,1)\). Apply each transformation to both points, and draw the six points \(\vec{a},\vec{b},\vec{a}R_1,\vec{b}R_1,\vec{a}R_2,\vec{b}R_2\) in the same co-ordinate system.
- Are they both rigid-body transformations (rotation)?
- If they are not rotations, what are they then?
Exercises from Ma (2003)
If you have time to spare, when you have done the exercises above, I recommend the following ones from Ma 2004 page 38ff.
- Exercise 2.1 a+d. (See Definition A.12 page 446.)
- Exercise 2.3. (See Definition A.13 page 447.)
More mathematical links
Consider the two vectors \(\vec{x}=[x_1,x_2,x_3]\) and \(\vec{y}=[y_1,y_2,y_3]\), and an orthonormal basis \(\vec{e}_1, \vec{e}_2, \vec{e}_3\).
- Write the inner product \([x_1,x_2,x_3]\cdot[y_1,y_2,y_3]\).
- Write the vectors as linear polynomials \(\vec{x}=x_1\vec{e}_1+ x_2\vec{e}_2+ x_3\vec{e}_3\) and \(\vec{y}=y_1\vec{e}_1+ y_2\vec{e}_2+ y_3\vec{e}_3\), and calculate the product \(\vec{x}\cdot\vec{y}\), using
- polynomial multiplication
- and the rules for the product \(\vec{e}_i\cdot\vec{e}_j\) for orthonormal bases.
- Are the two definitions of multiplication equivalent or different?
