Exercises

Equivalence of Points (Based on Exercise 3.1.)

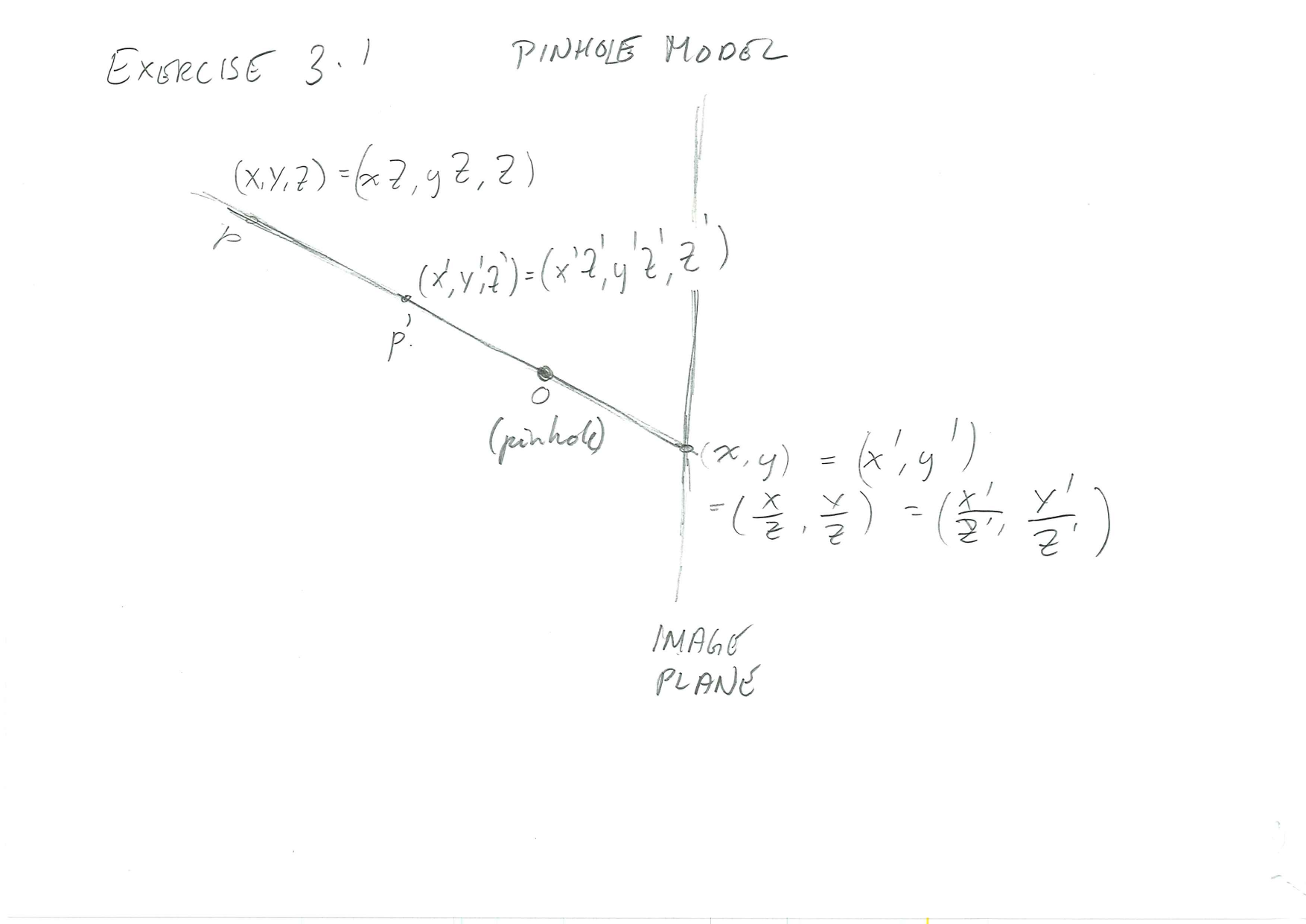
Note that the thin lens model is similar since rays through the centre of the lens (optical centre) are not deflected, and thus serves the role of a pinhole.

(Exercise 3.2)

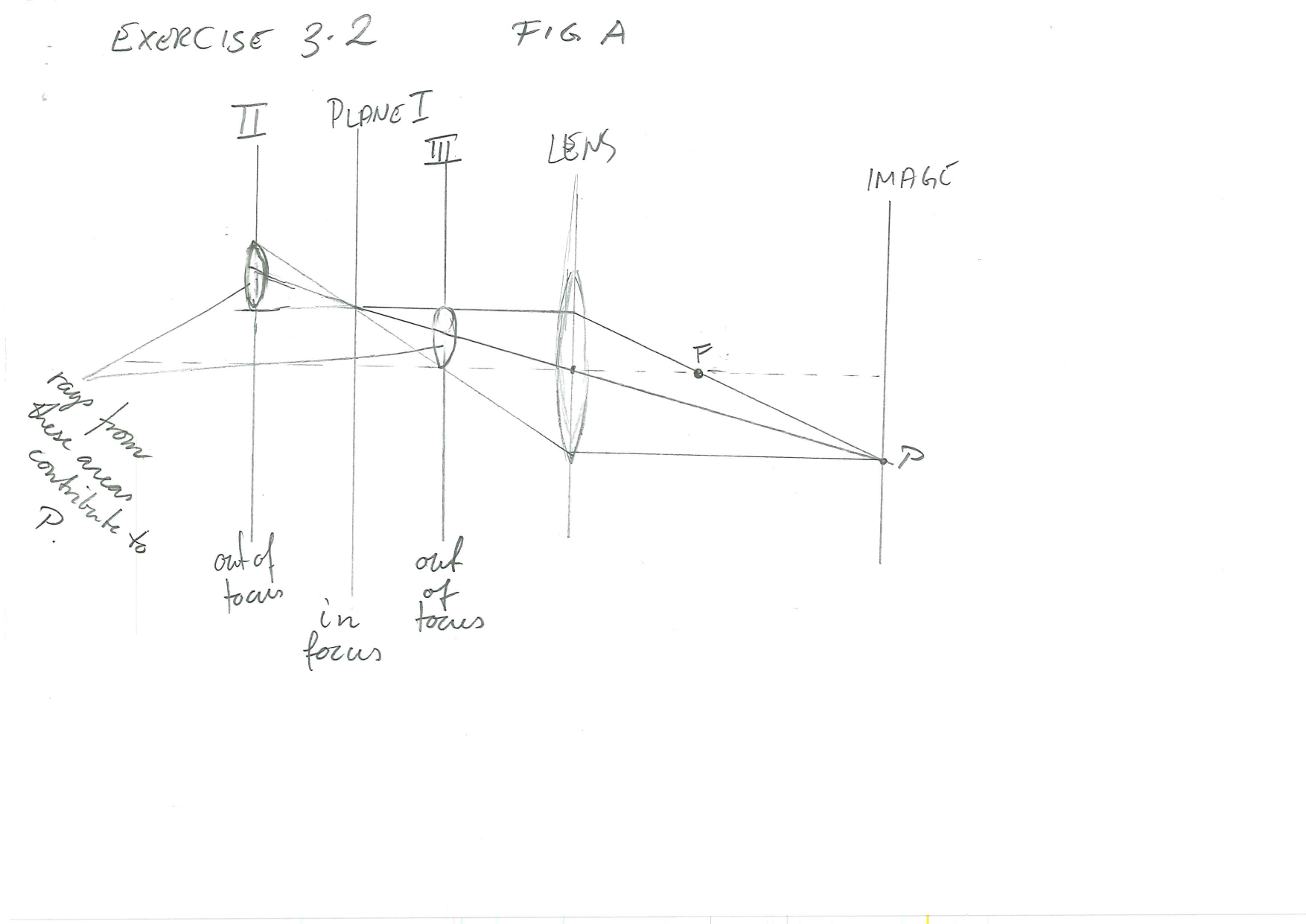
This initial figure is slightly inaccurate. Horizontal lines (object to lens, and lens to image point) delimit the region of interest. In reality it is the aperture that delimits the bundle of light that contributes to the image.

However it was my first impression of a possible solution, and if we just image that the aperture just happens to extend exactly to cover the rays drawn, then it is fine. Let’s redraw.

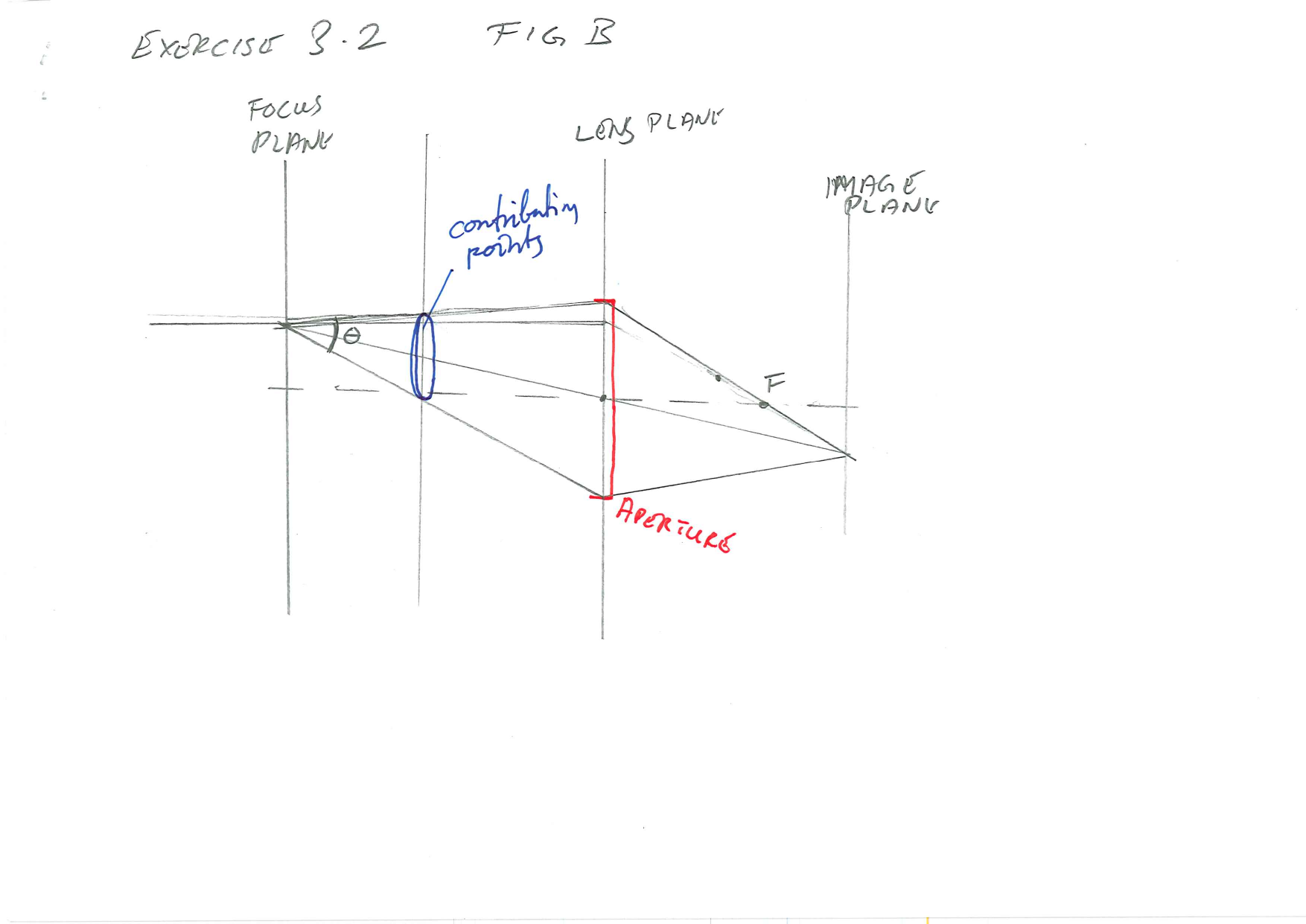
This figure shows the bundle of light emanating from the object point in the focus plane and passing through the apperture. Assuming that the aperture is is circular, the bundle is a skew cone, and the points contributing to the image point from the out-of-focus plane is a section of the skew cone.

This may sound as if we have to dig deep into Geometry and not only read the theory of conic sections but also the extensions to skew cones. Luckily, it is a lot simpler. Let’s redraw the figure, naming the points for ease of discussion.

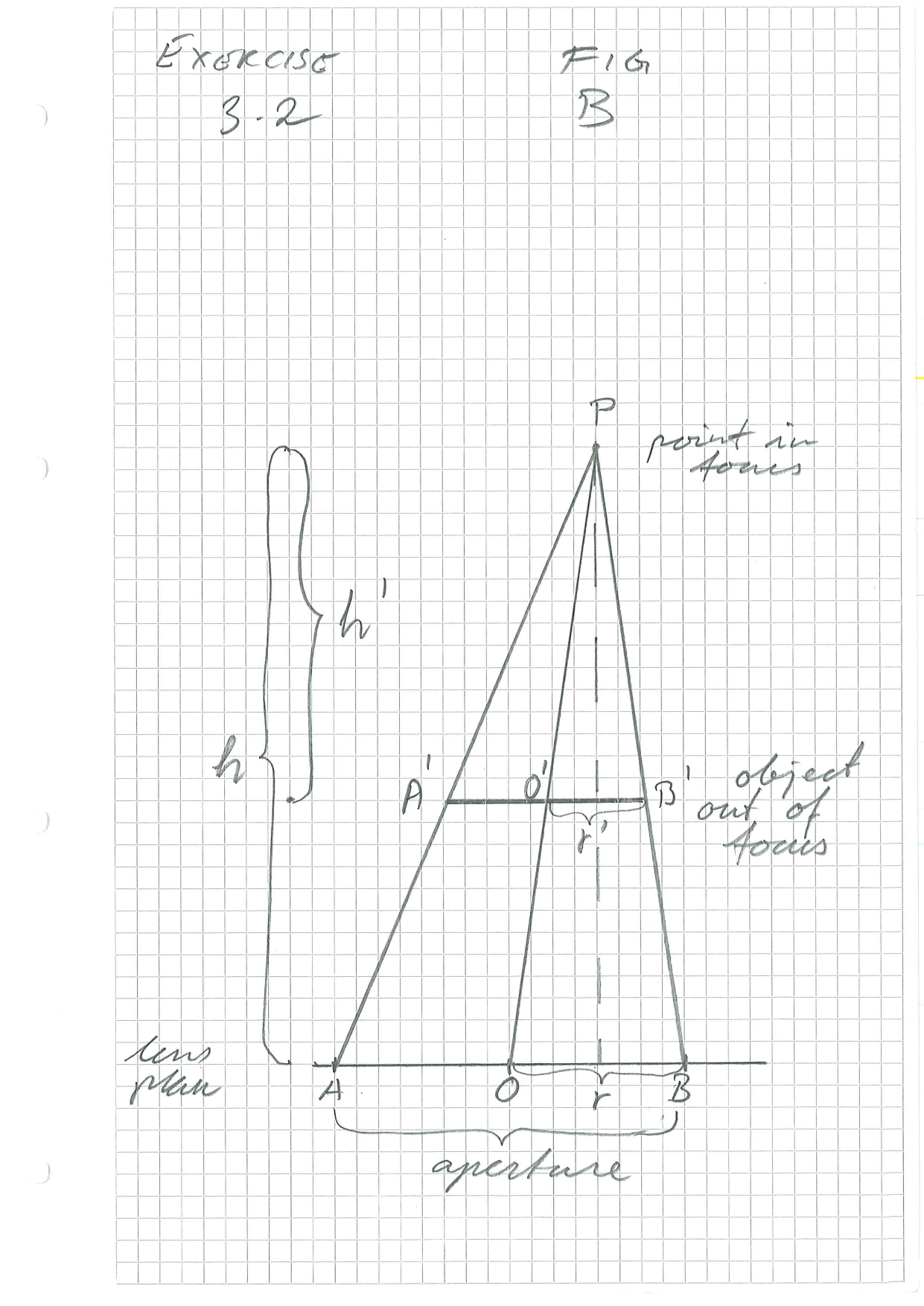
We see only a cross-section through the top \(P\) and the centre \(O\) of the base, but the argument can be made with any such cross section. The sections \(AO\) and \(BO\) are equal to the radius of the aperture in every cross-section, and the aperture is a circle, so the radius is always the same. Thus, even if the angle at \(P\) is different, the lengths \(AO\) and \(BO\) are constant.

We know that \(A'B'\) is parallell to \(AB\). Hence the triangles \(A'B'P\) and \(ABP\) are equivalent. The same is the case for \(A'O'P\) versus \(AOP\) and \(B'O'P\) versus \(BOP\). It follows that the ratio of the heights is equal to the ratio of the bases, that is: \[\frac{h'}{h} = \frac{A'O'}{AO} = \frac{B'O'}{BO}\] Since \(AO=BO=r\) is the radius of the aperture, \(A'O'=B'O'\) is the radius of the object. Hence the object forms a circle with radius \(r'=A'O'=B'O'\).
This gives \[\frac{h'}{h} = \frac{r'}{r}\] or \[r'=\frac{h'}{h}\cdot r\] Hence the object that contributes to the image of \(P\) is a circle with radius \(r'=h'r/h\), where \(h'\) is the distance between the focus plane and the object plane.

I agree that this exercise is tricky, in the sense that the solution is not at all obvious at the start. If you expect to find a template solution you are stuck. I had to make each of the figures in turn without knowing where I would be heading next, just to earn a little more insight into the problem each time. To succeed, you have to focus on understanding the geometry, rather than finding a computational procedure.

Scale Ambiguity (Exercise 3.8).

Use the figure from Exercise 3.1. Ask if it does not suffice.

Exercise 3.3 Part 1-2.